SIMULATION EINER SCHWEBEFÄHRE
Projektkontext und Ziel
Die „Schwebefähre“ ist eine besondere Fähre, die an Laufkatzen unterhalb einer Brücke aufgehängt ist (z.B. Rendsburg). In diesem Simulationsprojekt wurde das Schwingungsverhalten einer solchen Fähre modelliert. Ziel war es, die Bewegungsgleichungen (2. Ordnung) unter Berücksichtigung der hängenden Aufhängung herzuleiten und in Simulink nachzubilden. Der Fokus lag auf der dynamischen Analyse – z.B. wie die Fähre bei Wellengang oder durch Wind schwingen würde.
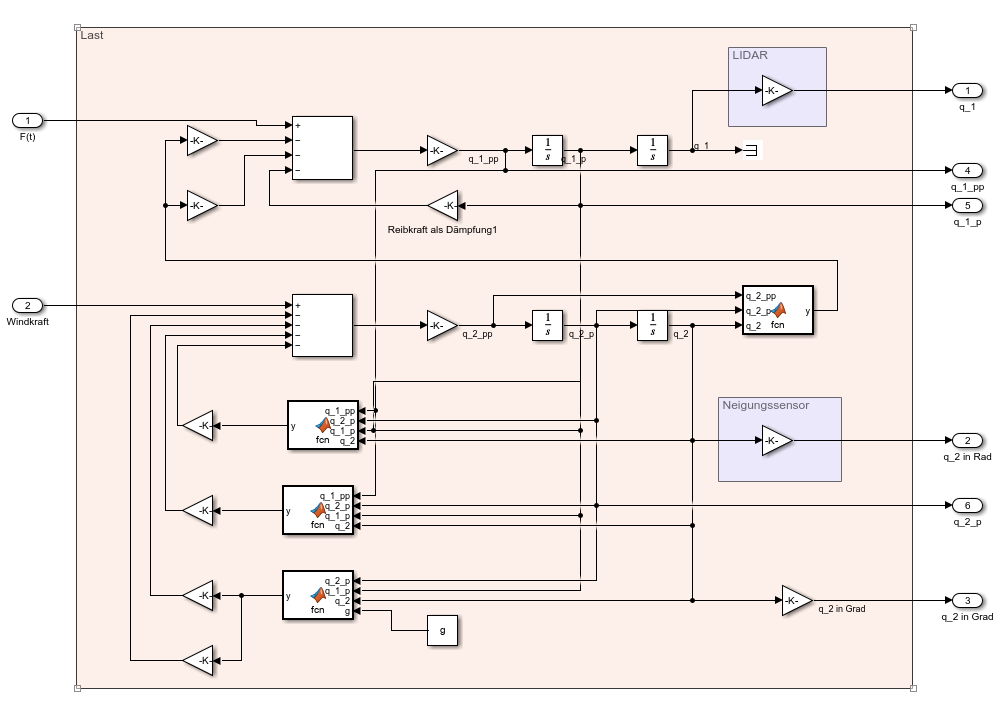
Technischer Aufbau und Methodik
Zunächst wurden die Bewegungsgleichungen mithilfe der Lagrange’schen Gleichungen zweiter Art aufgestellt (einschließlich Masse, Feder- und Dämpfungsparametern). Es entstand ein System gekoppelter Differentialgleichungen für die Vertikal- und Drehbewegung. Anschließend wurde ein Simulink-Modell erstellt, das diese Gleichungen löst. Hierzu kamen Integrator-Blöcke, Summen- und Gain-Blöcke zum Einsatz. Die Modellstruktur ist modular aufgebaut: Einerseits gibt es einen Block zur Berechnung der Kräfte (z.B. Federkräfte) und andererseits Blöcke zur Integration der Bewegung. Die komplette Simulation wurde in MATLAB/Simulink umgesetzt.
Werkzeuge / Software / Hardware
Für die Simulation wurde MATLAB R202x mit Simulink genutzt. Simulink bietet Bibliotheken für das direkte Lösen von Differentialgleichungen (z.B. Integrator, Scope). Zur Herleitung der Gleichungen kamen symbolische Tools oder manuelle Ableitung zum Einsatz. Die Visualisierung der Ergebnisse erfolgte in MATLAB mit plot-Funktionen. Ein normaler Entwicklungsrechner genügt, da die Simulationen (nur ein oder zwei Freiheitsgrade) rechnerisch unkritisch sind.
Ergebnisse / Besonderheiten
Die Simulation lieferte typische Schwebefähren-Bewegungen: ein unterlegtes, gedämpftes Oszillieren um die Gleichgewichtslage. Die Graphen zeigen die Schifflage (Nickwinkel) und Höhe über Zeit. Die Resultate stimmten mit physikalischen Erwartungen überein: beispielsweise wurde klar, dass eine höhere Dämpfung das Schwingungsamplituden schnell abklingen lässt. Eine besondere Herausforderung war die Kopplung zwischen translatorischer und rotatorischer Bewegung, was im Modell durch gekoppelte Blöcke gelöst wurde. Das Verhalten eines gedämpften Schwingungssystems wurde erfolgreich simuliert und zeigt typische Merkmale eines gedämpften Schwingungssystems.
Persönlicher Beitrag
Ich habe alle Schritte selbst durchgeführt: von der Herleitung der Gleichungen (händisch mittels Lagrange-Formalismus) über die Umsetzung in einem Simulink-Modell bis zur Auswertung der Ergebnisse. Insbesondere der Entwurf des modularen Simulink-Modells war aufwändig: Jeder Teil (Masse, Feder, Dämpfer) wurde als Block modelliert und verknüpft. Zur Visualisierung der Daten schrieb ich MATLAB-Skripte, die die Zeitreihen der Nick- und Hubbewegungen aufplotteten.
Bedeutung / Lernerfahrung / Ausblick
Das Projekt demonstriert mein Verständnis für physikalische Systemmodellierung und die Übersetzung mechanischer Gesetze in eine Simulationsumgebung. Ich konnte meine Kenntnisse im Umgang mit Simulink vertiefen und lernte, wie sich ein reales System (Schwebefähre) mithilfe von Differentialgleichungen beschreiben lässt.
Technische Zeichnungen
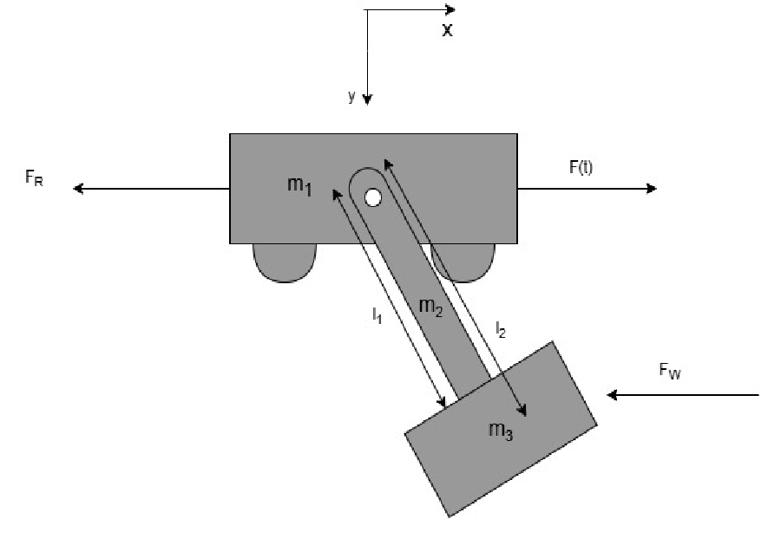
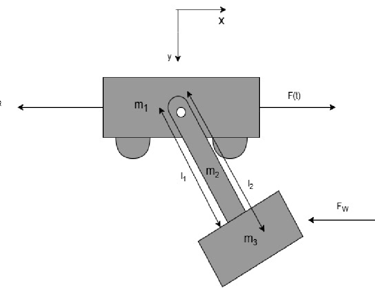
Abstraktion
Abstraktion des Systems zur dynamischen Untersuchung
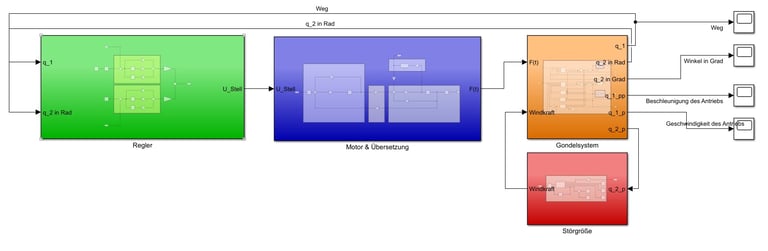
Gesamtsystem
Blockschaltbild des Gesamtssystems
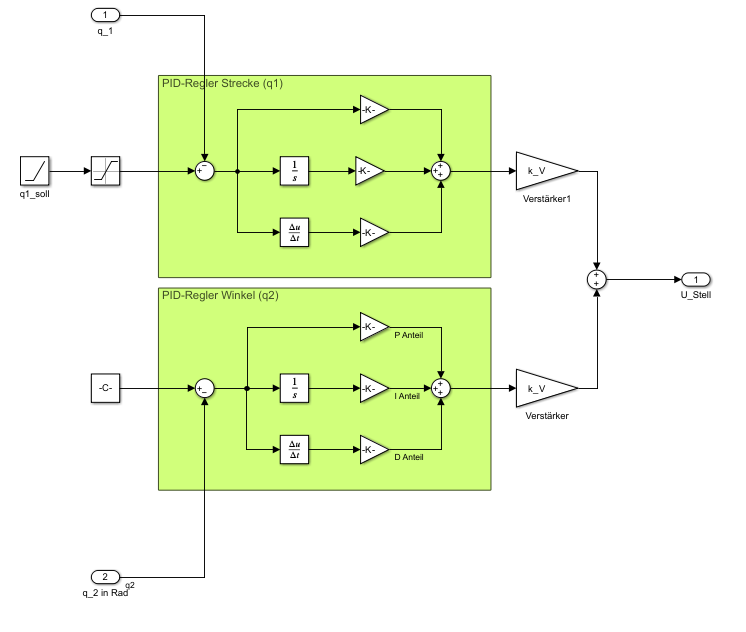
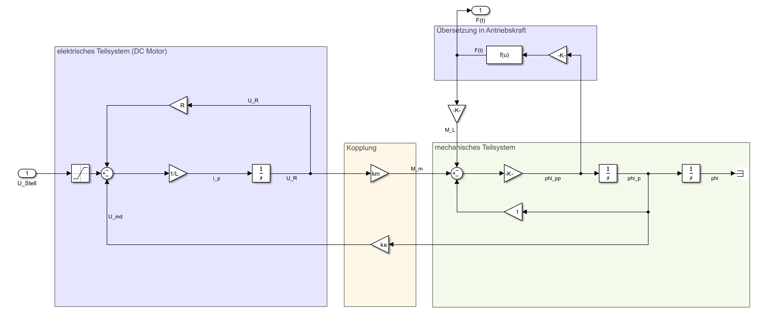
PID-Regler
Simulink Modell der PID-Regler
Antrieb
Simulink Modell des Antriebssystem
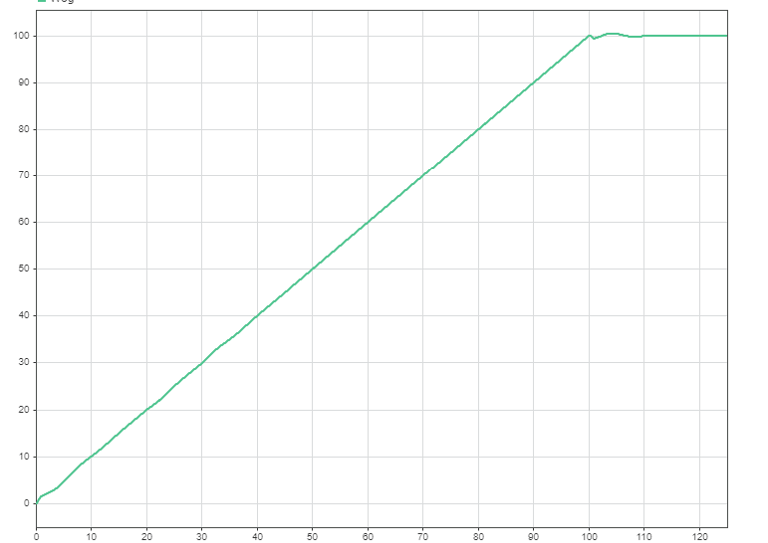
Weg
Verlauf der Weg mit der Zeit
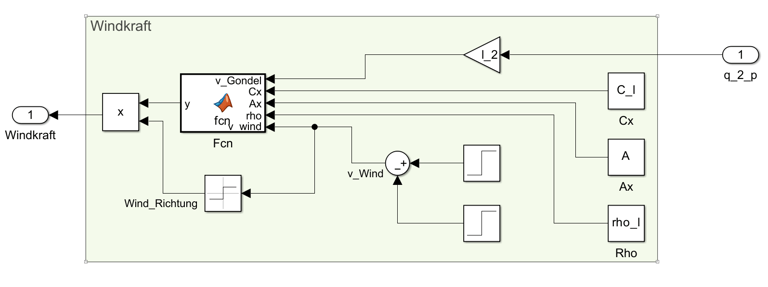
Störgröße
Simulink Modell der Störgröße
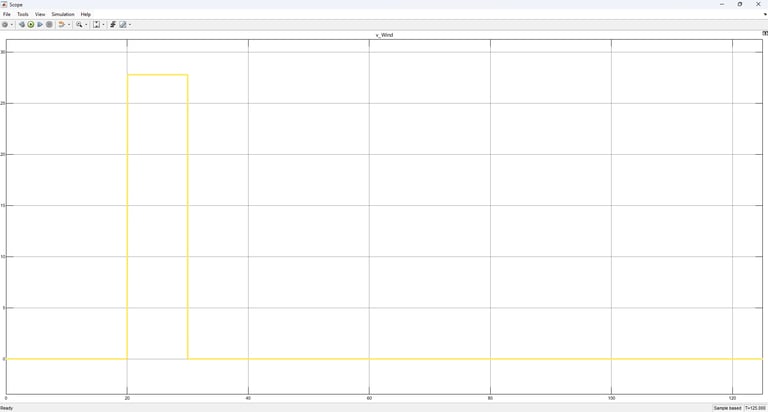
Störgröße
Windimpuls von 100 km/h
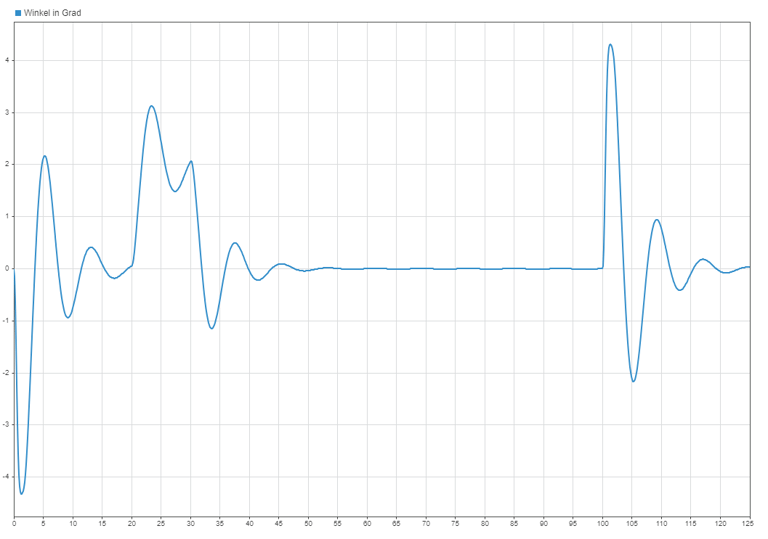
Schwingung
Schwingungswinkel der Gondel auf Grund der horizontalen Bewegung
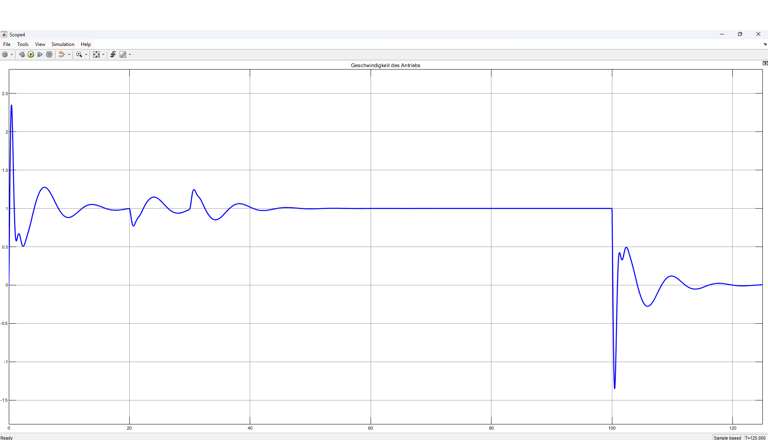
Geschwindigkeit
Horizontale Geschwindigkeit des Antriebssystem mit Wirkung der Störgröße
Kontakt
ngoune@yvandiran.com
+49 174 8271219
© 2025. Yvan D. NGOUNE. All rights reserved.
